Dynamic OD Departure Time Rescheduling (HADES)¶
One of the common reactions a traveler will make to congestion in a transport network is to change their departure time to ensure they still arrive at their destination at the required time. The effect is to spread the loading on the transport network and extend the period at which the network operates at, or near, capacity.
HADES¶
HADES (Heterogeneous Arrival and Departure Times with Equilibrium Scheduling) is an algorithm developed on behalf of the UK Dept. for Transport. It models micro time choice for arrival time at a destination where time shifts are typically measured in tens of minutes. The principle behind HADES is that a traveler has a preferred arrival time and that there is a scheduling cost associated with arriving early or late. The traveler will then try to minimize the total cost of the journey, including the scheduling cost, by adjusting their departure time.
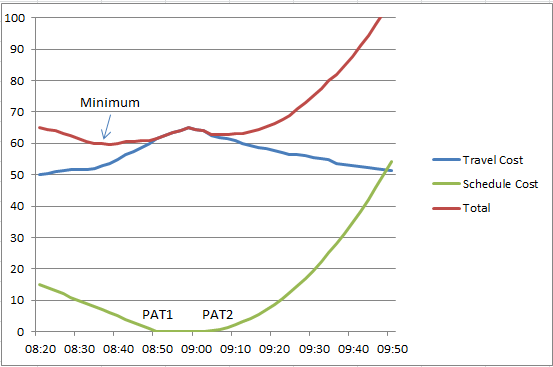
For example: A traveler can have a Preferred Arrival Time (PAT) of 9:00 AM and a travel cost of between 50 and 65 minutes where an arrival time of 08:20 requires a 50 minute journey and an arrival time of 09:00 requires a 65 minute journey due to increased congestion. In this case, the traveler associates a scheduling cost of 0 for arriving up to 10 minutes early,a linearly increasing scheduling cost for arriving earlier than 8:50 (PAT1- Preferred Arrival Time 1) and an exponentially increasing scheduling cost for arriving later than 9:00 (PAT2- Preferred Arrival Time 2). In this case, as illustrated below, the optimum time for the traveler to arrive at the destination is 8:40 to minimize the total of travel time costs and schedule costs.
The generalized cost is therefore:

where:
- \(t\): is the arrival time.
- \(PAT1\) and \(PAT2\) are the start and end of the arrival time window.
- α: is a cost coefficient for travel duration.
- \(T(t)\): is the travel duration for an arrival time t.
- \(f_1()\) and \(f_2()\) are scheduling cost functions for early and late arrival respectively.
Travel Times¶
For each iteration as the HADES algorithm re-assigns demand, a travel time is required which will vary according to the trip departure time and provide a detailed profile of the change in travel duration over time. These times are derived from a Mesoscopic Dynamic User Equilibrium which is run using a DUE experiment in each iteration.
HADES also requires default travel times for a set of PAT windows to determine the departure time in a base scenario for an arrival in each Preferred Arrival time slice. These times are derived from a .apa file generated from a base scenario.
Scheduling Costs¶
The scheduling cost is derived from a Function which evaluates the cost based on the difference between the arrival time and PAT1 and PAT2. This function can be a simple asymmetric linear function reflecting the perception that arriving early carries less of a scheduling cost than arriving late or it can be an exponential function reflecting the perception that the penalty for arriving late accumulates more rapidly as the delay increases.
The scheduling cost function should take into account the segmentation by User Class and Trip Purpose of the trip and also the time of day of the trip. For example, it might be important to arrive at work before 9:00 and to adjust the departure time to achieve that, but it might be less important to arrive home after work by a fixed time and no dynamic OD departure time rescheduling would be required.
Iteration¶
Once the initial travel times have been determined and the scheduling costs programmed, Aimsun Next uses an iterative process to reallocate demand between time periods using a Method of Successive Averages (MSA) approach.
- Run a Meso DUE to assign trips to the network and derive trip times.
- Calculate the cost of arrival in each arrival time window.
- Allocate the trip demand to arrival time windows.
- Adjust demand by allocating trips with a lower cost to a different arrival time window and hence a different departure time.
- Repeat until convergence criteria are met.
Demand adjustment is carried out using a Method of Successive Averages. First, for each OD pair and for each demand segment the demand is assigned to :
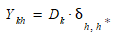
where:
- \(k\) is the preferred PAT window.
- \(h\) is the actual arrival window.
- \(D_k\) is the demand for an OD pair and user class combination with a target arrival time window k.
- δ 1 if the trip arrives in the arrival window \(h\) which corresponds to the PAT window \(h*\) with the lowest combined cost, 0 otherwise.
- \(Y_{kh}\) is therefore the demand for an OD pair and user class combination with a target window \(k\) that arrives in window \(h*\) which gives it the lowest cost.
The MSA algorithm then adjusts the demand as follows:
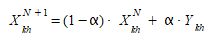
where:
- \(X^{N}_{kh}\) is the current adjusted demand in iteration \(N\) for each OD pair and user class with a target arrival time window \(k\) and arrival window \(h\).
- \(X^{N+1}_{kh}\) is the new adjusted demand in iteration \(N+1\).
- α is the step length.
Convergence¶
The convergence criteria are based on a delta gap function aggregated over each OD pair (\(i j\)) and user class (\(c\)):

where \(C_{ijckh}\) is the cost of travel for OD trip \(i-j\) for a vehicle in class \(c\) with a preferred PAT window \(k\) and an actual arrival window \(h\).