Dynamic OD Departure Time Rescheduling Experiment

The dynamic OD departure time rescheduling process modifies a traffic demand to adjust the departure time for trips such that vehicles arrive at their preferred arrival time despite differences in their journey times due to varying congestion in new scenarios. Changes in departure time are made, which are of the same order of time as the segmentation of time in the Traffic Demand specified in the modeled scenario. For example, if the Traffic Demand in a base scenario is composed of OD matrices at 10 minute intervals, as would be generated by a Static OD Departure Adjustment Scenario, then the Dynamic Departure Time Rescheduling Experiment will be able to reschedule demand in a future, more congested, scenario to give travelers a profile of arrival times that corresponds to the base scenario in steps of 10 minutes.

The theory behind Dynamic OD Departure Time Rescheduling experiment is described in the Theory Section.

Process

The Dynamic OD Departure Time Rescheduling Experiment requires three inputs:

• A Dynamic Scenario with a disaggregated Traffic Demand where the OD matrices define departure windows as well as defining the time profile of the demand. This scenario represents the future year test where, because of congestion, journey times have increased.

• A Path Assignment Object generated in a base scenario. This scenario represents the current year, calibrated with observed profile data, where travelers are assumed to finish trips at their preferred arrival time.

• Arrival Penalty Functions to add a "cost" of arriving early or late at a destination.

A Dynamic OD Departure Time Rescheduling Result will run a Mesoscopic DUE assignment and adjust the demand using a Method of Successive Averages to minimize the cost for trips and converge on a solution where minimal changes are made to the OD matrices.

The time interval used in the rescheduling experiment should be considered. It is implicitly set in the Traffic Demand and is based on the observable profile of flows in the real data used to calibrate the model. If the interval is set too long, the time differences supplied to the penalty functions will be large and the resulting high costs will mask any changes in journey times. In general time intervals should be small to allow for small time increments in rescheduling. However if they are too short, there is a risk of overfitting the departure time profile to data which contains stochastic noise, noise which is averaged in longer periods.

Dynamic OD Departure Time Rescheduling Experiment

A Dynamic OD Departure Time Rescheduling Experiment is created as an experiment in a Dynamic Scenario. A Dynamic OD Departure Time Rescheduling Result is created under the experiment to run the adjustment.

The experiment has the same tabs and controls for a Mesoscopic DUE as the assignment is done using a Meso DUE. There is one extra tab to control the rescheduling process.

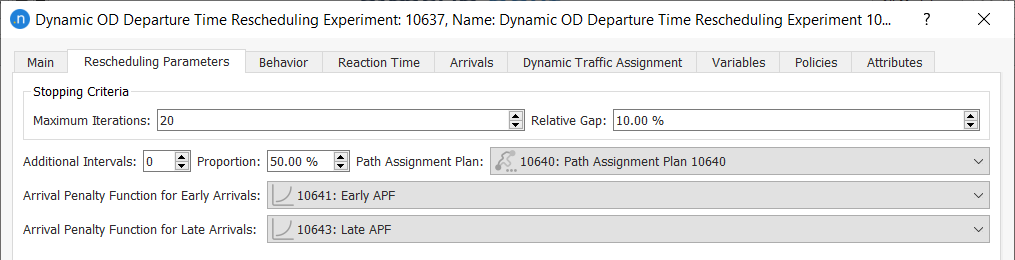
The Rescheduling Parameters tab specifies the maximum number of iterations, the convergence gap, and additional intervals at the start and end of the modeled period to accept those trips which now depart or arrive outside the originally modeled period.

The Rescheduling Parameters tab also specifies the Path Assignment object used to define the base times, the arrival penalty functions and the proportion of trips in the base matrices that can be moved between time intervals.

Running a Dynamic OD Departure Time Rescheduling Experiment

The Dynamic OD Departure Time Rescheduling Experiment Result is the object that runs the experiment. The result object is used to specify the random seed, or multiple random seeds if these are required to control the variability in the model using Mesoscopic Simulation Model Random Seeds.

The results of the experiment are the changes in the OD matrices which can be saved as a new demand object and associated matrices.

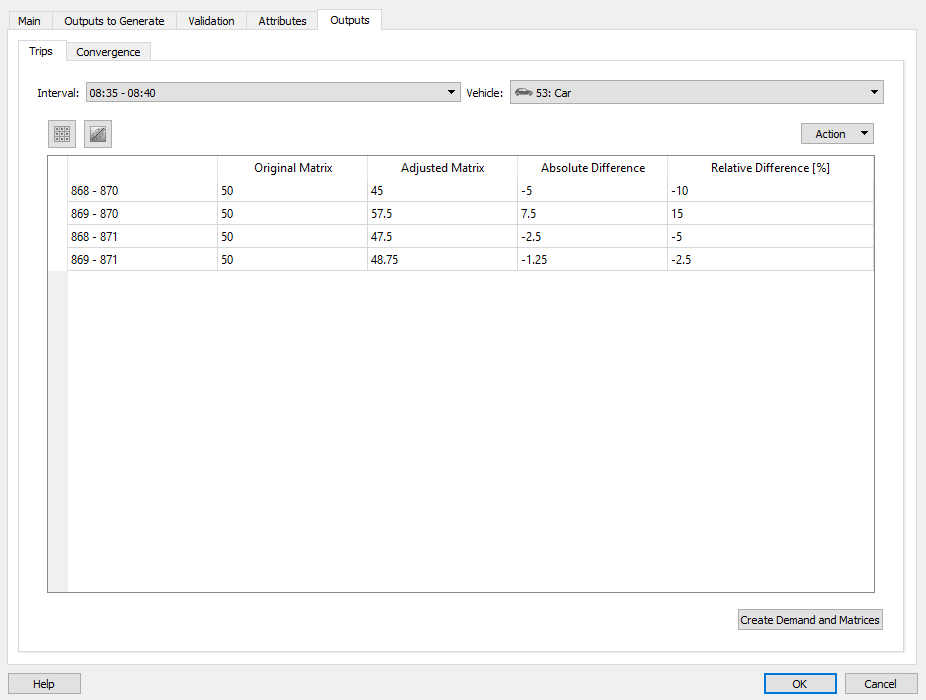
The results tab also provides a view of the experiment results showing the Rgap values for each iteration.